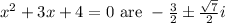Question

What is the solution to the following equation? x^2+3x+4=0

A) x=1; x=-3
B) x=3; x=-1
C) x= -3+- square root of -7/ 2
D) x= 3+- square root of 25/2

Answer 1

Option C

The solution of equation x^2+3x+4=0 is x= -3+- square root of -7/ 2

Solution:

Need to identify correct option for solution of the equation x^2 + 3x + 4 = 0.

Given equation is quadratic equation. We can find solution of this equation using quadratic formula.

According to quadratic formula for general equation
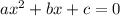`a x^(2)+b x+c=0` solution of the equation is given by

`x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

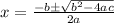
The given equation is
`x^(2)+3 x+4=0` So in our case, a = 1, b = 3 and c = 4

On applying quadratic formula we get

`\begin{array}{l}{x=\frac{-3 \pm \sqrt{3^(2)-4 * 1 * 4}}{2 * 1}} \\\\ {x=(-3 \pm √(9-16))/(2)} \\\\ {x=(-3 \pm √(-7))/(2)} \\\\ {x=-(3)/(2) \pm ((√(-1) * √(7)))/(2)}\end{array}`

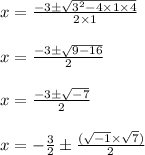
As i is square root of -1,

`\Rightarrow x=-(3)/(2) \pm (√(7))/(2) i`

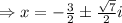
Hence correct option is C that is roots of quadratic equation
`x^(2)+3 x+4=0 \text { are }-(3)/(2) \pm (√(7))/(2) i`

Answer 2

x =−3±i√7/2

is the correc anwer