Question

Find the slope between the points (10, -1) and (-8, 6) 5/2 −7/18 2/5 −18/7

Answer 1

-7/18

Explanation:

hope It helps

Answer 2

The slope between the points (10, -1) and (-8, 6) is
`(-7)/(18)`

Solution:

Given, two points are (10, -1) and (-8, 6)

We have to find the slope of a line that, passes through the above given two points.

Now, we know that, slope of a line that passes through the points
`\left(\mathrm{x}_(1), \mathrm{y}_(1)\right) \text { and }\left(\mathrm{x}_(2), \mathrm{y}_(2)\right)`

`\mathrm{m}=(y_(2)-y_(1))/(x_(2)-x_(1))`

`\text { Here in our problem, } x_(2)=10, y_(2)=-1, x_(1)=-8 \text { and } y_(1)=6`

`\text { Then, slope } m=(-1-6)/(10-(-8))=(-1-6)/(10+8)=(-7)/(18)`

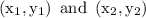
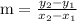
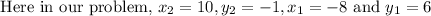
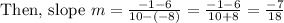
Hence, the slope of a line that passes through the given two points is
`(-7)/(18)`