Question

The vertex is (-3,3) and goes through point (-2,6). What is equation in vertex form.

Answer 1

The vertex is (-3,3) and goes through point (-2,6). The equation in vertex form is
`y=3(x+3)^(2)+3`

Solution:

Given that, vertex of a parabola is (-3, 3) and the parabola passes through the point (-2, 6).

We have to find the equation of parabola in vertex form.

The general form of parabola equation in vertex form is given as:

`y=a(x-h)^(2)+k`

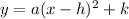
Where (h, k ) is vertex and a is a constant .

Here in our problem, h = -3 and k = 3

Then, parabola equation is given as:

`y=a(x-(-3))^(2)+3 \rightarrow y=a(x+3)^(2)+3`

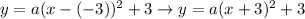
Now, we know that it passes through (-2, 6). So substitute x = -2 and y = 6

`\rightarrow 6=a(-2+3)^(2)+3 \rightarrow a(1)^(2)=6-3 \rightarrow a=3`

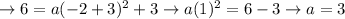
So, now parabola equation in vertex form is
`y=3(x+3)^(2)+3`