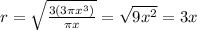Question

The volume of a cone is 3 X cubic units and its height is x units.

Which expression represents the radius of the cone's base, in units?
3x
0 6x
34x2
gax?

Answer 1

The complete questions says:

The volume of a cone is
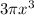`3\pi x^3` cubic units and its height is x units.

Which expression represents the radius of the cone's base, in units?

Answer:

3x

Explanation:

The volume of a cone is given by:

`V=(1)/(3)\pi r^2 h`

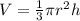
where

r is the radius of the base

h is the heigth of the cone

In this problem, we know:

The volume of the cone:

`V=3\pi x^3` (1)

And its height:

`h=x` (2)

We can re-arrange the formula above to make r, the radius, the subject:

`r=\sqrt{(3V)/(\pi h)}`

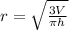
And by substituting (1) and (2), we find the radius:

`r=\sqrt{(3(3\pi x^3))/(\pi x)}=√(9x^2)=3x`