Question

33. Suppose you were on a planet where the

acceleration of gravity was only 2.0 m/s2 instead
of 9.8 m/s2 as on Earth. (a) Estimate the height
to which you could jump vertically from a
standing start if you can jump to 0.75 m on
Earth. (b) How high could you throw a baseball
if you could throw it 18 meters up on Earth?

Answer 1

a) 3.675 m

b) 3.67m

Step-by-step explanation:

We are given acceleration due to gravity on earth =
`9.8ms^-2`

And on planet given =
`2.0ms^-2`

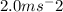
A) Since the maximum jump height is given by the formula

`\mathrm{H}=\frac{\left(\mathrm{v} 0^(2) * \sin 2 \emptyset\right)}{2 \mathrm{g}}`

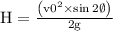
Where H = max jump height,

v0 = velocity of jump,

Ø = angle of jump and

g = acceleration due to gravity

Considering velocity and angle in both cases

`\frac{\mathrm{H} 1}{\mathrm{H} 2}=\frac{\mathrm{g} 2}{\mathrm{g} 1}`

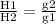
Where H1 = jump height on given planet,

H2 = jump height on earth = 0.75m (given)

g1 = 2.0
`ms^-2` and

g2 = 9.8
`ms^-2`

Substituting these values we get H1 = 3.675m which is the required answer

B) Formula to find height of ball thrown is given by

`\mathrm{h}=(\mathrm{v} 0 * \mathrm{t})+\frac{\mathrm{a} *\left(t^(2)\right)}{2}`

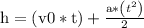
which is due to projectile motion of ball

Now h = max height,

v0 = initial velocity = 0,

t = time of motion,

a = acceleration = g = acceleration due to gravity

Considering t = same on both places we can write

`\frac{\mathrm{H} 1}{\mathrm{H} 2}=\frac{\mathrm{g} 1}{\mathrm{g} 2}`

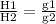
where h1 and h2 are max heights ball reaches on planet and earth respectively and g1 and g2 are respective accelerations

substituting h2 = 18m, g1 = 2.0
`ms^-2` and g2 = 9.8
`ms^-2`

We get h1 = 3.67m which is the required height