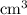Slant height of tetrahedron is=6.53cm
Volume of the tetrahedron is=60.35
Given:
Length of each edge a=8cm
To find:
Slant height and volume of the tetrahedron
Step by Step Explanation:
Solution;
Formula for calculating slant height is given as
Slant height=
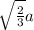
Where a= length of each edge
Slant height=
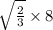
=
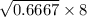
=
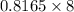 =6.53cm
=6.53cm
Similarly formula used for calculating volume is given as
Volume of the tetrahedron=

Substitute the value of a in above equation we get
Volume=
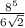
=
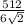
=
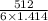
Volume=
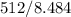 =60.35
=60.35
Result:
Thus the slant height and volume of tetrahedron are 6.53cm and 60.35