Question

A ball is kicked from the top of a building with a velocity of 50 m/s and lands 165 m away from the base of the buildi

C) What is the vertical velocity of the ball when it hits the ground?

Answer 1

32.3 m/s

Step-by-step explanation:

The ball follows a projectile motion, where:

- The horizontal motion is a uniform motion at costant speed

- The vertical motion is a free fall motion (constant acceleration)

We start by analyzing the horizontal motion. The ball travels horizontally at constant speed of

`v_x = 50 m/s`

and it covers a distance of

d = 165 m

So, the total time of flight of the ball is

`t=(d)/(v_x)=(165)/(50)=3.3 s`

In order to find the vertical velocity of the ball, we have now to analyze its vertical motion.

The vertical motion is a free-fall motion, so the ball is falling at constant acceleration; therefore we can use the following suvat equation:

`v_y = u_y +at`

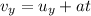
where

`v_y` is the vertical velocity at time t

`u_y=0` is the initial vertical velocity

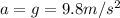`a=g=9.8 m/s^2` is the acceleration of gravity (taking downward as positive direction)

Substituting t = 3.3 s (the time of flight), we find the final vertical velocity of the ball:

`v=0 + (9.8)(3.3)=32.3 m/s`