Answer:
The required probability is calculated as 0.052
Solution:
As per the question:
The probability that people dropped out in the first 4 weeks of the program, p = 0.25
The size of the sample, n = 246
Now,
To calculate the Probability of at least 195 people being in the program after first 4 weeks:
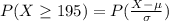 (1)
(1)
where
 = mean
= mean
 = standard deviation
= standard deviation
X = No. of people still part of the program
Now,
Mean can be given as:
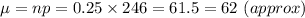
The mean no. of people still part of the program = 246 - 62 = 184
Standard deviation is given by:
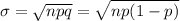
where
q = 1 - p = 1 - 0.25 = 0.75
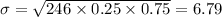
Now, using the appropriate values in eqn (1):
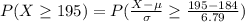
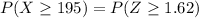
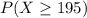 = 1 - P(Z < 1.62)
= 1 - P(Z < 1.62)
Using Z-table:

Thus the required probability is calculated as 0.052