Question

Learning Goal: To practice Problem-Solving Strategy 4.1 for projectile motion problems. A rock thrown with speed 12.0 m/s and launch angle 30.0 ∘ (above the horizontal) travels a horizontal distance of d = 15.5 m before hitting the ground. From what height was the rock thrown? Use the value g = 9.800 m/s2 for the free-fall acceleration.

Answer 1

the height was thrown = 1.938 m

Step-by-step explanation:

given,

speed of the rock = 12 m/s

angle of launch = 30.0 ∘

horizontal distance = d = 15.5 m

acceleration due to gravity = 9.8 m/s²

`u_x = u cos \theta`

`u_x = 12 cos 30^0`

`u_x = 10.39 m/s`

`u_y = u sin \theta`

`u_y = 12 sin 30^0`

`u_y = 6 m/s`

`time = (s_x)/(u_x)`

`time = (15.5)/(10.39)`

t = 1.49 s

`s_y = u_y t + (1)/(2)gt^2`

`s_y = 6* 1.49 - (1)/(2)* 9.8 * 1.49^2`

`s_y = -1.938 m`

hence, the height was thrown = 1.938 m

Answer 2

The height from which the rock was thrown is 1.92 m

Solution:

As per the question:

Speed with which the rock is thrown, v = 12.0 m/s

Horizontal distance traveled by the rock before it hits the ground, d = 15.5 m

Launch angle,
`\theta = 30.0^(\circ)`

Now,

To calculate the height, h from which the rock was thrown:

First, since we consider the horizontal motion in the trajectory of the rock, thus the time taken is given by:

`t = (d)/(vcos\theta)`

`t = (15.5)/(12.0cos30.0^(\circ)) = 1.49\ s`

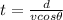
Now,

The height from which the rock was thrown is given by the kinematic eqn, acceleration in the horizontal direction is zero:

`h = vsin\theta t - (1)/(2)gt^(2)`

`h = 12.0sin30.0^(\circ)* 1.49 - (1)/(2)* 9.8* 1.49^(2) = - 1.92\ m`