Question

Use the method of Lagrange multipliers to find the dimensions of the rectangle of greatest area that can be inscribed in the ellipse StartFraction x squared Over 25 EndFraction plusStartFraction y squared Over 16 EndFraction equals1 with sides parallel to the coordinate axes.

Answer 1

5sqrt(2)

4sqrt(2)

Explanation:

Answer 2

Answer with Step-by-step explanation:

Let a rectangle box whose dimensions are u and v.Then,
`(u/2, v/2)`

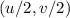
must lie on the ellipse

Given equation of ellipse

`(x^2)/(25)+(y^2)/(16)=1`

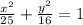
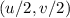`(u/2,v/2)`must lie on the circle therefore,

`(u^2)/(100)+(v^2)/(64)=1`

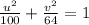
with
`u,v\geq 0`

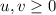
Suppose , we have to maximize a function
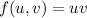`f(u,v)=uv` subject to constraints g(u,v)=
`(u^2)/(100)+(v^2)/(64)=1`

`\\abla f=<v,u> \\abla g=<(u)/(50),(v)/(32) >`

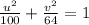
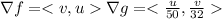
Using Lagrange multipliers method

`\\abla f=\lambda\\abla g`

`v=\lambda (u)/(50)`

`u=\lambda(v)/(32)`

`\lambda=(50v)/(u)=(32u)/(v)`

`50v^2=32u^2`

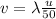
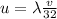
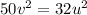
if u=0 then v=0 g(u,v)=
`0\\eq 1`

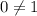
It is absurd condition.

Therefore, we take u and v >0

`v^2=(32u^2)/(50)=(16)/(25)u^2`

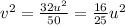
Substitute the value in ellipse equation then we get

`(u^2)/(100)+(u^2)/(100)=1`

`(2u^2)/(100)=1`

`u^2=50`

`u=5 \sqrt2`

`v^2=(16)/(25)* 50=32`

`v=4\sqrt2`

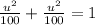
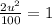
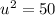
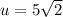
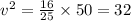
The critical point is (
`5\sqrt2, 4\sqrt2)`.

Therefore, we concluded that the dimensions of the rectangle of greatest area is attained by choosing a box of dimensions
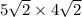`5\sqrt2 * 4\sqrt2`.