Answer:
Circumcenter is
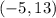 .
.
Explanation:
Given:
The three vertices of triangle OVW are
 .
.
Circumcenter is a point inside the triangle which is equidistant from each of the vertices of the triangle.
Let
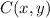 be the circumcenter.
be the circumcenter.
Distance between two points
 and
and
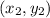 is given as:
is given as:
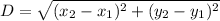
So, as per the definition of circumcenter, distance of point
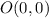 from point
from point
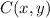 is equal to distance of point
is equal to distance of point
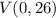 from point
from point
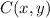 .
.
So, OC = VC
or
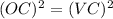
 .
.
Similarly, distance of point
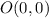 from point
from point
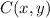 is equal to distance of point
is equal to distance of point
 from point
from point
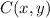 .
.
 or
or
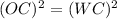
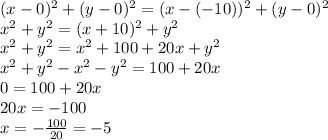 .
.
Therefore, the circumcenter of the triangle with the given vertices is
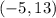 .
.