Answer:
10.8 units.
Explanation:
Given:
Centers of two circles are
 and
and
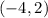 .
.
Distance between two points
 and
and
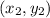 is given as:
is given as:
Distance,
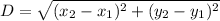
Here,
 is
is
 and
and
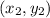 is
is
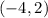 .
.
Plug in these values and calculate the distance between these 2 points.
Distance between the centers is given as:

Therefore, the distance between the centers of the two circles is 10.8 units.