Question

What initial investment must be made to accumulate $60000 in 17 years if the money is invested in a mutual fund that pays 12% annual interest, compounded monthly?

Answer 1

$7881.18

Explanation:

Let the initial Investment be
`P_(0)`. The Interest is compounded on a monthly basis at 12% annual interest rate. After 17 years, the Investment amounts to $60,000.

As the annual interest rate is 12%, the monthly interest rate is 1%.

Since this is a compound interest problem, the total amount can be modeled as follows:
`P(t)=P_(0)(1+(i)/(100))^(t)`

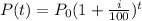
Here
`i` is the interest rate, i.e
`1`, and t is the number of time periods, i.e
`17\textrm{ years x }12\frac{\textrm{months}}{\textrm{year}}`=
`204\textrm{ months}`

`60,000=P_(0)\textrm{ x }((101)/(100))^(204)`

`P_(0)=7881.18`

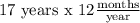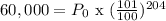
∴ Initial Investment = $7881.18