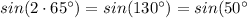Answer:
A. 65 degrees
Step-by-step explanation:
The formula to calculate the range of a projectile is:
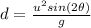
where
u is the initial speed of the projectile
g is the acceleration of gravity
 is the angle of projection of the projectile
is the angle of projection of the projectile
We want to find the angle
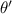 such that it has the same range of a projectile fired at
such that it has the same range of a projectile fired at
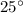 , therefore:
, therefore:
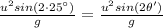
It follows that
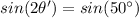
And there are two angles that satisfies this condition:
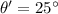
and
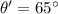
In fact, with the second choice,