Answer:
The absolute minimum of the surface area function on the interval
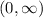 is
is
![S(2\sqrt[3]{15})=12\cdot \:15^{(2)/(3)} \:ft^2](https://img.qammunity.org/2020/formulas/mathematics/college/9vkwoue7jd2rgtma9dshsnix30bqlhsn98.png)
The dimensions of the box with minimum surface area are: the base edge
![x=2\sqrt[3]{15}\:ft](https://img.qammunity.org/2020/formulas/mathematics/college/3fc9fkb89j8i59zp40kmjhv6we68yvhek3.png) and the height
and the height
![h=\sqrt[3]{15} \:ft](https://img.qammunity.org/2020/formulas/mathematics/college/opoa0sgsctmxf90wch2jdv14gv7zjryly7.png)
Explanation:
We are given the surface area of a box
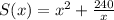 where x is the length of the sides of the base.
where x is the length of the sides of the base.
Our goal is to find the absolute minimum of the the surface area function on the interval
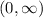 and the dimensions of the box with minimum surface area.
and the dimensions of the box with minimum surface area.
1. To find the absolute minimum you must find the derivative of the surface area (
 ) and find the critical points of the derivative (
) and find the critical points of the derivative (
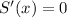 ).
).
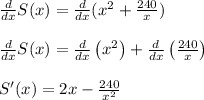
Next,
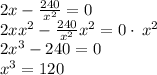
There is a undefined solution
 and a real solution
and a real solution
![x=2\sqrt[3]{15}](https://img.qammunity.org/2020/formulas/mathematics/college/nw84isxctxyo5s5zgpybvavs39tp3rw5oh.png) . These point divide the number line into two intervals
. These point divide the number line into two intervals
![(0,2\sqrt[3]{15})](https://img.qammunity.org/2020/formulas/mathematics/college/m5mdgdixx2avm620pecbmrycj4yg97bvqm.png) and
and
![(2\sqrt[3]{15}, \infty)](https://img.qammunity.org/2020/formulas/mathematics/college/v558kpka40fvw8gjltbebafp2jj49bg1vg.png)
Evaluate S'(x) at each interval to see if it's positive or negative on that interval.
![\begin{array}{cccc}Interval&x-value&S'(x)&Verdict\\(0,2\sqrt[3]{15}) &2&-56&decreasing\\(2\sqrt[3]{15}, \infty)&6&(16)/(3)&increasing \end{array}](https://img.qammunity.org/2020/formulas/mathematics/college/72hr1tv0gl9pegjgbm28l2tblprdqseopz.png)
An extremum point would be a point where f(x) is defined and f'(x) changes signs.
We can see from the table that f(x) decreases before
![x=2\sqrt[3]{15}](https://img.qammunity.org/2020/formulas/mathematics/college/nw84isxctxyo5s5zgpybvavs39tp3rw5oh.png) , increases after it, and is defined at
, increases after it, and is defined at
![x=2\sqrt[3]{15}](https://img.qammunity.org/2020/formulas/mathematics/college/nw84isxctxyo5s5zgpybvavs39tp3rw5oh.png) . So f(x) has a relative minimum point at
. So f(x) has a relative minimum point at
![x=2\sqrt[3]{15}](https://img.qammunity.org/2020/formulas/mathematics/college/nw84isxctxyo5s5zgpybvavs39tp3rw5oh.png) .
.
To confirm that this is the point of an absolute minimum we need to find the second derivative of the surface area and show that is positive for
![x=2\sqrt[3]{15}](https://img.qammunity.org/2020/formulas/mathematics/college/nw84isxctxyo5s5zgpybvavs39tp3rw5oh.png) .
.

and for
![x=2\sqrt[3]{15}](https://img.qammunity.org/2020/formulas/mathematics/college/nw84isxctxyo5s5zgpybvavs39tp3rw5oh.png) we get:
we get:
![2+\frac{480}{\left(2\sqrt[3]{15}\right)^3}\\\\\frac{480}{\left(2\sqrt[3]{15}\right)^3}=2^2\\\\2+4=6>0](https://img.qammunity.org/2020/formulas/mathematics/college/m1kfnob9rfvqr2k1ggxrktenl7vz7adj8q.png)
Therefore S(x) has a minimum at
![x=2\sqrt[3]{15}](https://img.qammunity.org/2020/formulas/mathematics/college/nw84isxctxyo5s5zgpybvavs39tp3rw5oh.png) which is:
which is:
![S(2\sqrt[3]{15})=(2\sqrt[3]{15})^2+\frac{240}{2\sqrt[3]{15}} \\\\2^2\cdot \:15^{(2)/(3)}+2^3\cdot \:15^{(2)/(3)}\\\\4\cdot \:15^{(2)/(3)}+8\cdot \:15^{(2)/(3)}\\\\S(2\sqrt[3]{15})=12\cdot \:15^{(2)/(3)} \:ft^2](https://img.qammunity.org/2020/formulas/mathematics/college/29cepf3qejmcypuxw1zrrn8yn7sannbn2l.png)
2. To find the third dimension of the box with minimum surface area:
We know that the volume is 60
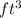 and the volume of a box with a square base is
and the volume of a box with a square base is
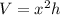 , we solve for h
, we solve for h
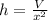
Substituting V = 60
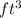 and
and
![x=2\sqrt[3]{15}](https://img.qammunity.org/2020/formulas/mathematics/college/nw84isxctxyo5s5zgpybvavs39tp3rw5oh.png)
![h=\frac{60}{(2\sqrt[3]{15})^2}\\\\h=\frac{60}{2^2\cdot \:15^{(2)/(3)}}\\\\h=\sqrt[3]{15} \:ft](https://img.qammunity.org/2020/formulas/mathematics/college/vapths7nctlw7tswndp97i5vlrk770lopt.png)
The dimension are the base edge
![x=2\sqrt[3]{15}\:ft](https://img.qammunity.org/2020/formulas/mathematics/college/3fc9fkb89j8i59zp40kmjhv6we68yvhek3.png) and the height
and the height
![h=\sqrt[3]{15} \:ft](https://img.qammunity.org/2020/formulas/mathematics/college/opoa0sgsctmxf90wch2jdv14gv7zjryly7.png)