Question

Juan's cell phone company charges $35 a month for phone service plus $0.50 for each text message. How many text messages does juan send in a month if his bill was $52

Answer 1

34

Explanation:

The minimum charges for the phone service is $35. For, each text message, $0.50 is charged over and above the minimum charges.

This problem can be modeled as a linear equation in the number of text messages sent as follows:
`\textrm{Total bill = Minimum charges + (Charge per message)x(Number of messages)}`

`\textrm{Total Bill = $}35\textrm{ + (Number of messages)x}($0.50)`

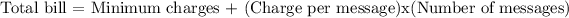
Given that the total bill is $52, number of text messages can be easily computed.

`52\textrm{ = }35+\textrm{(Number of messages)x}0.50`

`\textrm{(Number of messages)x0.50 = }52-35=7`

`\textrm{Number of messages = }(7)/(0.5)=14`

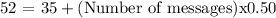
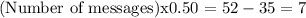
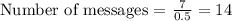
∴Number of text messages Juan sent = 14.