Answer:
Explanation:
In this problem we have:
The statement
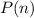 : Every positive integer
: Every positive integer
 can be written as a sum of distinct powers of two.
can be written as a sum of distinct powers of two.
We need to prove two steps:
1.Base Case : Prove that the statement
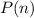 holds when
holds when
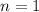 .
.
Induction Hypothesis : Assume that for all positive integers less than or equal to
 , the statement holds.
, the statement holds.
2. Inductive Step : Prove, using the Induction hypothesis, that must
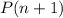 be true.
be true.
Proof:
1.Base case: Since
 then the statement
then the statement
 holds.
holds.
2.Inductive Step:
Fix a positive integer
 and suppose that
and suppose that
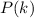 holds for all
holds for all
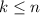 .
.
Case 1:
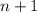 is even, then
is even, then
 is an integer and we have that
is an integer and we have that
 , then
, then
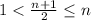 . Since
. Since
 , by the inductive hypothesis, there exists
, by the inductive hypothesis, there exists
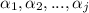 such that
such that
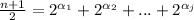 and
and
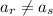 for every
for every
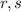 ∈
∈
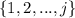 . Then
. Then

All elements of the set
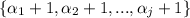 are distinct. Suppose that there exists
are distinct. Suppose that there exists
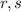 ∈
∈
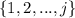 such that
such that
 , then subtracting 1 from both sides of this equation, we get
, then subtracting 1 from both sides of this equation, we get
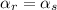 , this is a contradiction because we are assuming that all the powers
, this is a contradiction because we are assuming that all the powers
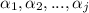 are distinct. Therefore the statement holds when
are distinct. Therefore the statement holds when
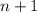 is even.
is even.
Case 2:
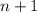 is odd.
is odd.
In this case
 is even, by the inductive hypothesis we know that
is even, by the inductive hypothesis we know that
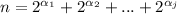 , then
, then
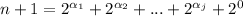 . Since
. Since
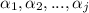 are all distinct, we only need to prove that 0 ∉
are all distinct, we only need to prove that 0 ∉
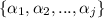 .
.
If there exists
 ∈
∈
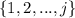 such that
such that
 , then
, then
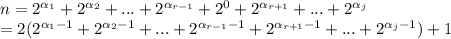
but this is a contradiction because
 is even, therefore
is even, therefore
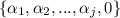 are distinct powers and the statement holds when
are distinct powers and the statement holds when
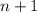 is odd. Therefore, the statement that every positive integer
is odd. Therefore, the statement that every positive integer
 can be written as a sum of distinct powers of two holds for all positive integer.
can be written as a sum of distinct powers of two holds for all positive integer.