Answer:
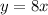
Explanation:
Given:
Distance cycled by Brenna for 1 trip =
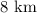
Total number of trips =

Total distance cycled for
 trips =
trips =

∵ Distance cycled for 1 trip =
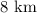
∴ Distance cycled for
 trips =
trips =
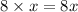
But, distance cycled for
 trips =
trips =
 .
.
So,
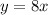 .
.
Therefore, the relationship between the number of trips to work
 and the total distance cycled
and the total distance cycled
 is
is
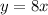 .
.