Question

Total freshman = 58. Number of freshman who prefer cheese toppings= 14. Determined the probability that a freshman prefer cheese toppings. Round to the nearest thousandth

Answer 1

The probability that a freshman prefer cheese toppings is 0.241

Explanation:

Probability of any event E =
`\frac{\textrm{Number of favorable outcomes}}{\textrm{Total number of outcomes}}`

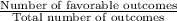
Here, let E : Event of choosing cheese toppings

So, the number of favorable outcomes = 14

Total number of outcomes = 58

So,
`P(E) =  \frac{\textrm{Number of students who like cheese toppings}}{\textrm{Total number of students}}`

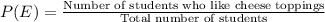
or, P(E) =
`(14)/(58) = 0.241379`

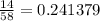
So,the probability that a freshman prefer cheese toppings is 0.241379

Rounding of 0.241379 to the nearest thousandth, we get

Here , in 0.241379 thousandth digit is 3, and 3 < 5,

so the value of P(E) = 0.241