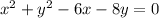Question

A circle passes through (3,-1),(-2, 4), and (6,8)

Using the standard form of a circle x2 + y2 + Dx+ Ey+ F = 0, fill in missing
numbers to create the system of equations.

Answer 1

D = -6, E = -8 , F = 0

Explanation:

standard form =
`x^(2) + y^(2) + Dx + Ey + F = 0`

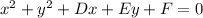
now, when circle passes through (3,-1);

⇒
`3^(2) + (-1)^(2) + D(3) + E(-1) + F = 0`

⇒
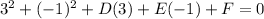
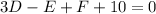`3D - E + F + 10 = 0` ...............( equation 1)

when circle passes through (-2,4);

⇒
`(-2)^(2) + 4^(2) + D(-2) + E(4)+ F = 0`

⇒
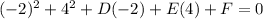
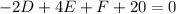`-2D + 4E + F + 20 = 0` ...............( equation 2)

when circle passes through (6,8);

⇒
`6^(2) + 8^(2) + D(6) + E(8) + F = 0`

⇒
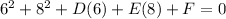
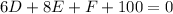`6D + 8E + F + 100= 0` ................( equation 3)

by solving these 3 equations , we get;

D = -6, E = -8, F = 0

hence,

standard form =
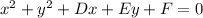
`x^(2) + y^(2) + Dx + Ey + F = 0`

=
`x^(2) + y^(2) - 6x - 8y = 0`