Question

A movie theater is filled to its capacity of 350. The theater charges $4.50 for children, $7.50 for students, and $12.50 for adults. There are half as many adults as there are students. If the total ticket sales was $2415, how many children, students, and adults attended. Write your answer as an ordered triple in the form (# of children, # of students, # of adults). For example, (1,2,3).

Answer 1

(170;120;60).

Explanation:

We know that:

Capacity of the theater: 350 people.

Adults is half the students.

Children's cost: $4.50

Student's cost: $7.50

Adults' cost: $12.50

Total Sales: $2415

We are gonna call x the children, y the students and z the adults:

So, the equation to express the capacity of the theater would be:

`x+y+z=350`

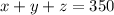
But,
`z=(y)/(2)` (adults are have students)

So, the expression would be:
`x+y+(y)/(2) =350`

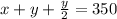
Solving y's and Isolating x :

`x+(3y)/(2) =350\\x=350-(3y)/(2)`

Now, we need a expression for costs. We have:

`4.50x+7.50y+12.50z=2415`

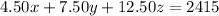
Replacing the x and z equation:

`4.50(350-(3y)/(2) )+7.50y+12.50(y)/(2)=2415`

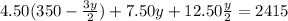
Now, we solve for y:

`1575-6.75y+7.50y+6.25y=2415\\07y=2415-1575\\7y=840\\y=(840)/(7) =120`

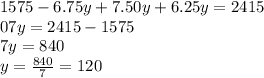
But, we know that adults are half as many students, so:

`z=(y)/(2)=(120)/(2) =60`

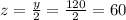
Lastly,

`x+y+z=350\\x+120+60=350\\x=350-120-60\\x=170`

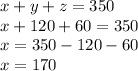
Therefore, there are 170 children, 120 students and 60 adults. Expressing the results as an ordered triple would be (170;120;60)