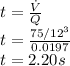Question

A mold has a downsprue length = 6.0 in. The cross sectional area at the bottom of the sprue is 0.5 in2. The sprue leads into a horizontal runner which feeds the mold cavity, whose volume = 75 in3. Determine (a) velocity of the molten metal flowing through the base of the downsprue, (b) volume rate of flow, and (c) time required to fill the mold cavity.

Answer 1

a) To calculate the velocity of the molten metal we need to apply the conservative energy equation,

`V=√(2gl)V=\sqrt{2(32.2)((6)/(12))}`

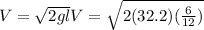
*Note I am converting all to feet.

`V=6.6745ft/s`

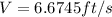
b)To calculate the volume flow we only use the equation of Discharge, so

`Q=AV\\Q=((0.5)/(12^2))(5.6745)\\Q=0.0197ft^3/s`

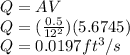
c) To calculate the time we use the equation of Discharge but in terms of Velocity, that is,

`t=\frac{\dot{V}}{Q} \\t=(75/12^3)/(0.0197)\\t=2.20s`