Answer:
Explanation:
for a damping system you have the regenerative force exerted by the spring and the term given by the resistance of the damper which is proportional to the speed of the block equal mass times acceleration
let m be the mass of the object, b the damper constant, and k the spring constant, so we have:
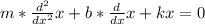
we replace in the previous equation to get:

we are going to find the roots of the previous equation, let
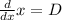
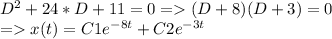
now for case a)
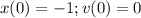
so we have to differentiate the expression:

for case a just replace the first initial condition in x(t) and the second in v(t)
 , then we have
, then we have
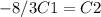
and -1= C1 -8/3C1 => C1 = 3/5 and C2 = -8/5
now for case b)
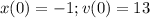
you have
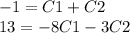
in this case C1 = -1-C2, then you replace in the second equation and you get
13 = -8*(-1-C2)-3C2 = 8+5C2 => C1 = -2 and C2 = 1