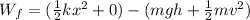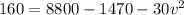Question

To practice Problem-Solving Strategy 7.2 Problems Using Mechanical Energy II. The Great Sandini is a 60.0-kg circus performer who is shot from a cannon (actually a spring gun). You don’t find many men of his caliber, so you help him design a new gun. This new gun has a very large spring with a very small mass and a force constant of 1100 N/m that he will compress with a force of 4400 N. The inside of the gun barrel is coated with Teflon, so the average friction force will be only 40.0 N during the 4.00 m he moves in the barrel. At what speed will he emerge from the end of the barrel, 2.50 m above his initial rest position?a. v1, initial speed b.Y2, final height c. F, magnitude of compressing force d. k, force constant of springe. l, distance traveled between nitial and final statef.Y1, initial heightg. f, magnitude of friction h. m, mass of body in motion i. v2, final speed

Answer 1

`v = 15.45 m/s`

Step-by-step explanation:

As per mechanical energy conservation we can say that here since friction is present in the barrel so we will have

Work done by friction force = Loss in mechanical energy

so we will have

`W_f = (U_i + K_i) - (U_f + K_f)`

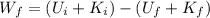
here we know that

`W_f = F_f . d`

`W_f = 40 * 4`

`W_f = 160 J`

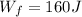
Initial compression in the spring is given as

`F = kx`

`4400 = 1100 x`

`x = 4 m`

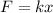
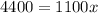
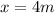
now from above equation

`W_f = ((1)/(2)kx^2 + 0) - (mgh + (1)/(2)mv^2)`

`160 = ((1)/(2)1100(4^2) + 0) - (60 * 9.8* 2.50 + (1)/(2)(60)v^2)`

`160 = 8800 - 1470 - 30 v^2`

`v = 15.45 m/s`