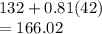Answer:
Explanation:
Given that the demand for the 6 p.m. flight from Toledo Express Airport to Chicago's O'Hare Airport on Cheapfare Airlines is normally distributed with a mean of 132 passengers and a standard deviation of 42
Let X be the no of passengers who report
X is N(132, 42)
Or Z is
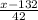
a) Suppose a Boeing 757 with a capacity of 183 passengers is assigned to this flight.
the probability that the demand will exceed the capacity of this airplane
=
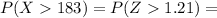
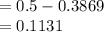
b) the probability that the demand for this flight will be at least 80 passengers but no more than 200 passengers
=
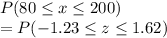
=0.4474+0.3907
=0.8381
c) the probability that the demand for this flight will be less than 100 passengers
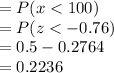
d) If Cheapfare Airlines wants to limit the probability that this flight is overbooked to 3%, how much capacity should the airplane that is used for this flight have? passengers
=
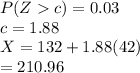
e) 79th percentile of this distribution
=