Answer: B) 0.0107
Explanation:
As per given , we have
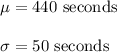
Let x be the random variable that represents the time for this event for boys in secondary school .
z-score =

z-score for x= 325 ,

Required probability :
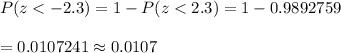
Hence, the probability that a randomly selected boy in secondary school can run the mile in less than 325 seconds = 0.0107