Answer:
a) The 95 percent confidence interval for the portion of respondents who feel the president is doing a good job is (0.5292, 0.5908).
b) The lower end of the confidence interval is above 0.5, so yes, it is reasonable to conclude that a majority (half) of the population believes the president is doing a good job.
Explanation:
The first step to solve this problem is building the confidence interval. If the lower end of the interval is above 0.5, it is reasonable to conclude that a majority of the population believes that the president is doing a good job.
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence interval
, and a confidence interval
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.
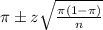
In which
Z is the zscore that has a pvalue of
 .
.
For this problem, we have that:
a)
A sample of 1000 voters was surveyed, and 560 feel that the president is doing a good job. This means that
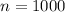 and
and
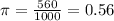 .
.
We have
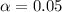 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
 = 0.975, so
= 0.975, so
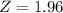 .
.
The lower limit of this interval is:
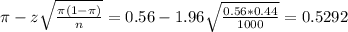
The upper limit of this interval is:
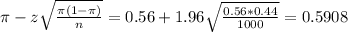
The 95 percent confidence interval for the portion of respondents who feel the president is doing a good job is (0.5292, 0.5908).
b) The lower end of the confidence interval is above 0.5, so yes, it is reasonable to conclude that a majority (half) of the population believes the president is doing a good job.