Question

In Northern Yellowstone Lake, earthquakes occur at a mean rate of 1.3 quakes per year. Let X be the number of quakes in a given year. (a) Justify the use of the Poisson model. Earthquakes are not independent events. Earthquakes occur at regular intervals. Earthquakes are random and independent events. (b) What is the probability of fewer than three quakes? (Round your answer to 4 decimal places.) Probability (c) What is the probability of more than five quakes? (Round your answer to 4 decimal places.) Probability

Answer 1

a) Earthquakes are random and independent events.

b) There is an 85.71% probability of fewer than three quakes.

c) There is a 0.51% probability of more than five quakes.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

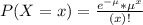
In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given time interval.

In this problem, we have that:

In Northern Yellowstone Lake, earthquakes occur at a mean rate of 1.3 quakes per year, so
`\mu = 1.3`

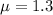
(a) Justify the use of the Poisson model.

Earthquakes are random and independent events.

You can't predict when a earthquake is going to happen, or how many are going to have in a year. It is an estimative.

(b) What is the probability of fewer than three quakes?

This is
`P(X < 3)`

`P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)`

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-1.3)*1.3^(0))/((0)!) = 0.2725`

`P(X = 1) = (e^(-1.3)*1.3^(1))/((1)!) = 0.3543`

`P(X = 2) = (e^(-1.3)*1.3^(2))/((2)!) = 0.2303`

`P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) = 0.2725 + 0.3543 + 0.2303 = 0.8571`

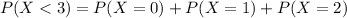
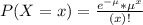
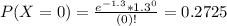
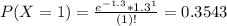
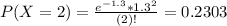
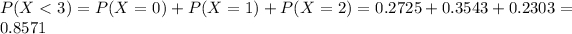
There is an 85.71% probability of fewer than three quakes.

(c) What is the probability of more than five quakes?

This is
`P(X > 5)`

We know that either there are 5 or less earthquakes, or there are more than 5 earthquakes. The sum of the probabilities of these events is decimal 1.

So

`P(X \leq 5) + P(X > 5) = 1`

`P(X > 5) = 1 - P(X \leq 5)`

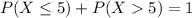
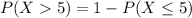
In which

`P(X \leq 5) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5)`

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-1.3)*1.3^(0))/((0)!) = 0.2725`

`P(X = 1) = (e^(-1.3)*1.3^(1))/((1)!) = 0.3543`

`P(X = 2) = (e^(-1.3)*1.3^(2))/((2)!) = 0.2303`

`P(X = 3) = (e^(-1.3)*1.3^(3))/((3)!) = 0.0980`

`P(X = 4) = (e^(-1.3)*1.3^(4))/((4)!) = 0.0324`

`P(X = 5) = (e^(-1.3)*1.3^(5))/((5)!) = 0.0084`

`P(X \leq 5) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) = 0.2725 + 0.3543 + 0.2303 + 0.0980 + 0.0324 + 0.0084 = 0.9949`

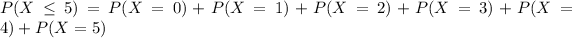
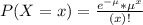
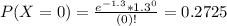
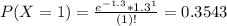
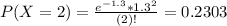
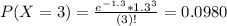
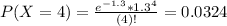
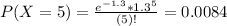
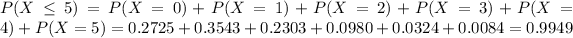
Finally

`P(X > 5) = 1 - P(X \leq 5) = 1 - 0.9949 = 0.0051`

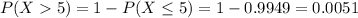
There is a 0.51% probability of more than five quakes.