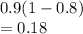Answer:
Explanation:
Given that a recent college graduate will take the first actuarial exam in June. The probability that she passes the first exam is .9. If she passes the first exam, then the conditional probability that she passes the second one is.8, and if she passes both the first and the second exams, then the conditional probability that she passes the third exam is .7
Since unless she clears one exam she cannot go for the next, we can say that
a) the probability that she passes all three exams=
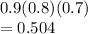
b) Given that she did not pass all three exams, what is the conditional probability that she failed the second exam
=Prob she passed in I and failed in II
=