Answer:
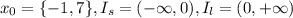
Explanation:
Remember that an IVP (initial value problem) of first order consists of solving a first-order differential equation (DE) and the solution
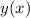 must satisfy the initial condition
must satisfy the initial condition
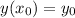 . This means that the solution y(x) must pass through the point on the plane
. This means that the solution y(x) must pass through the point on the plane
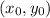 .
.
In this case, we know that
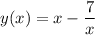 is already a solution of the DE xy'+y=2x, the value of
is already a solution of the DE xy'+y=2x, the value of
 and we have to find the values
and we have to find the values
 for which the equality
for which the equality
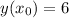 holds, that is,
holds, that is,
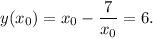
Multiplying by
 the above equation we obtain
the above equation we obtain
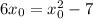 , where it follows by susbtracting
, where it follows by susbtracting
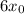 that
that
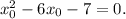 This is a second-degree polynomial equation and its solutions can be found by factoring:
This is a second-degree polynomial equation and its solutions can be found by factoring:
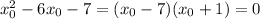 . Therefore, there are two possible values for
. Therefore, there are two possible values for
 : 7 and -1. From here we can see that -1 is the smaller and 7 is the larger.
: 7 and -1. From here we can see that -1 is the smaller and 7 is the larger.
Now, the larger interval
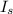 for which
for which
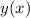 is a solution of the IVP
is a solution of the IVP
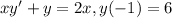 (the smaller value of
(the smaller value of
 ) is the maximal interval where y(x) is defined and pass through the point (-1,6). In this case, it must be that
) is the maximal interval where y(x) is defined and pass through the point (-1,6). In this case, it must be that
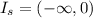 .
.
Finally, the larger interval
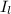 for which
for which
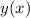 is a solution of the IVP
is a solution of the IVP
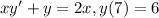 (the larger value of
(the larger value of
 ) is the maximal interval where y(x) is defined and pass through the point (7,6). In this case, it must be that
) is the maximal interval where y(x) is defined and pass through the point (7,6). In this case, it must be that
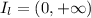 .
.