Question

A swimming pool whose volume is 10,000 gal contains water that is 0.01% chlorine. Starting at t = 0, city water containing0.001% chlorine is pumped into the pool at a rate of 5 gal/min. The pool water flows out at the same rate. What is thepercentage of chlorine in the pool after 1 h? When will the pool water be 0.002% chlorine?

Answer 1

The answer above is correct, it proves that the chlorine would take an estimate time.

Explanation:

Answer 2

a) The percentage of chlorine after 1 hour is 0.00973%.

b) The pool water will habe a concentration of 0.002% chlorine at 4394 minutes (or 73.24 hours).

Explanation:

We can define as X(t) the amount of chlorine that is in the pool at time t.

Then, the rate of change of X can be written as

`(dX)/(dt)=(rate\,in)-(rate\,out)\\ \\(dX)/(dt)=C_i*f_(in)-(X(t))/(10,000)*f_(out)`

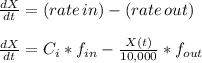
being Ci the concentration of chlorine of the inflow (0.001%), f_in the inflow (5 gal/min) and f_out the outflow (the same as the inflow, 5 gal/min).

`(dX)/(dt)=(0.001)/(100)*5-(X)/(10000)*5=(1)/(20000)-(X)/(2000)=-(X-0.1)/(2000)   \\\\(dX)/(X-0.1) =(-dt)/(2000)\\\\ln|X-0.1|=(-t)/(2000) +C\\\\X-0.1=C*e^(-t/2000)\\\\X=0.1+C*e^(-t/2000)`

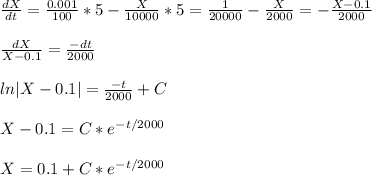
When t=0, the concentration is 0.01%, so the amount of chlorine X is

`X=(0.01)/(100)*10000=1\,gal`

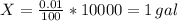
Replacing in the equation, we have

`X=0.1+C*e^(-t/2000)\\\\1=0.1+C*e^(-0/2000)=0.1+C*1\\\\C=0.9`

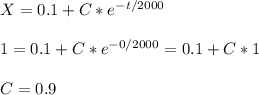
The amount of chlorine for any time t is then

`X(t)=0.1+0.9*e^(-t/2000)`

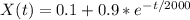
a) At one hour (t=60 min), the amount of chlorine is

`X(60)=0.1+0.9*e^(-60/2000)=0.1+0.9*0.9704=0.973`

This amount means a concentration of

`C=A/10000=0.973/10000=0.00973 \%`

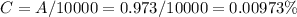
b) A concentration of 0.002% of chlorine means an amount of chlorine of

`X=(0.002/100)*10000=0.2\,gal`

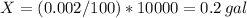
Then we can calculate

`X(t)=0.2=0.1+0.9*e^(-t/2000)\\\\e^(-t/2000)=(0.2-0.1)/0.9=0.1111\\\\-t/2000=ln(0.111)\\\\t=-2000*ln(0.1111)=4394\, min`