Question

Two vehicles approach a right angle intersection and then suddenly collide. After the collision, they become entangled. If their mass ratios were 1:4 and their respective speeds as they approached the intersection were both 13 m/s, find the magnitude and direction of the final velocity of the wreck.a. 11 m/s at 76° with respect to the original direction of the lighter car. b. 16 m/s at 76° with respect to the original direction of the lighter car. c. 16 m/s at 14° with respect to the original direction of the lighter car.d. 11 m/s at 14° with respect to the original direction of the lighter car. e. 26 m/s at 76° with respect to the original direction of the lighter car.

Answer 1

a. 11 m/s at 76° with respect to the original direction of the lighter car.

Step-by-step explanation:

In this exercise, since both cars make a right angle, let's assume that the lighter car only has a horizontal velocity component (vx) and that the heavier one only has a vertical velocity component (vy). The final velocities for both components for the system can be determined as:

`m_(1) v_(x1)+m_(2)v_(x2)=(m_(1)+m_(2))v_(fx)\\m_(1) v_(y1)+m_(2)v_(y2) =(m_(1)+m_(2))v_(fy)`

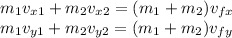
Assume that the lighter car has a 1kg mass and that the heavier car has a 4 kg mass.

`1*13 + 4*0 = (1+4) v_(fx)\\v_(fx)=(13)/(5) =2.6\\1*0 + 4*13 = (1+4) v_(fy)\\v_(fy)=(13*4)/(5) =10.4\\`

The magnitude of the final velocity of the wreck can be found as:

`v_(f)^(2)= v_(fx)^(2)+ v_(fy)^(2)\\v_(f)=\sqrt[]{2.6^(2) + 10.4^(2)} \\v_(f)= 10.72`

The final velocity has an intensity of roughly 11 m/s

As for the angle, it can be determined in respect to the lighter car (x axis) as follows:

`\theta = cos^(-1)((v_(fx) )/(v_(f)) )\\\theta = cos^(-1)((2.6)/(10.7) )\\\theta = 76^(o)`

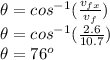
Therefore, the wreck has a velocity with an intensity of 11 m/s at 76° with respect to the original direction of the lighter car.