Question

Suppose a university advertises that its average class size is 34 or less. A student organization is concerned that budget cuts have led to increased class sizes and would like to test this claim. A random sample of 43 classes was​ selected, and the average class size was found to be 35.6 students. Assume that the standard deviation for class size at the college is 9 students. Using α=0.10​, complete part a below.

a. Does the student organization have enough evidence to refute the​ college's claim?

Determine the null and alternative hypotheses.

H0​: μ ____ (greater than or equals≥ less than or equals≤ greater than> not equals≠ equals= less than<)

H1​: μ ____ (equals= less than or equals≤ greater than or equals≥ less than< greater than> not equals≠)

The​ z-test statistic is ____

​(Round to two decimal places as​ needed.)

The critical​ z-score(s) is(are) ____.

​(Round to two decimal places as needed. Use a comma to separate answers as​ needed.)

Because the test statistic _____________ (does not fall within the critical values, is greater than the critical value, is less than the critical value, falls within the critical values)

______(do not reject, reject) the null hypothesis.

Enter your answer in the edit fields

Answer 1

H0​: μ ≤ 34

H1​: μ > 34

The​ z-test statistic is ≈ 1.8

The critical​ z-score is 1.28

we fail to reject the null hypothesis H0​: μ ≤ 34

Explanation:

H0​: μ ≤ 34

H1​: μ > 34

The​ z-test statistic is calculated using the formula:

z=
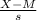`(X-M)/(s)` where

• X is the average class size found in the sample (35.6)
• M is the mean according to the null hypothesis (34)
• s is the standard deviation for class size (9)

then z=
`(35.6-34)/(9)` ≈ 0.18

The critical​ z-score is 1.28 for α=0.10​ (one tailed)

Because the test statistic is less than the critical value, do not reject the null hypothesis.