Answer:
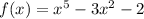 has 5 real and 0 non-real zeroes.
has 5 real and 0 non-real zeroes.
Explanation:
Here, the given polynomial is
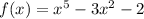
Now, by FUNDAMENTAL THEOREM OF ALGEBRA:
A polynomial of degree n can have at most n roots.
So, here the number of roots f(x) can have = 5
Now, examine the change in the sign of f(x) and f(-x)
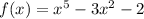
Signs of f(x) is + - -.
So for f(x) the sign changes only once.
Now,
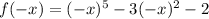
or,
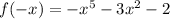
Here, signs are - - -
So,for f(-x) the SIGNS DO NOT CHANGE.
So it has no negative real zero.
Hence,
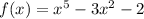 has 5 real and 0 non-real zeroes.
has 5 real and 0 non-real zeroes.