Question

H(t)=t² + 4t + 3

1) What are the zeros of the function?
Write the smaller t first, and the larger t second.
\text{smaller } = s, m, a, l, l, e, r.
\text{larger} = l, a, r, g, e, r.
2) What is the vertex of the parabola?

Answer 1

Explanation:

Answer 2

1) The zeros of the function is at t=-3,-1.

2) The vertex of the parabola is (-2,-1).

Explanation:

Given : Function
`h(t)=t^2+4t+3`

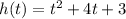
To find :

1) What are the zeros of the function?

2) What is the vertex of the parabola?

Solution :

1) The zeros of the function,

To find the roots of the equation, replace h(t)=0 and solve.

`t^2+4t+3=0`

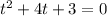
Applying middle term split,

`t^2+3t+t+3=0`

`t(t+3)+1(t+3)=0`

`(t+3)(t+1)=0`

`t=-3,-1`

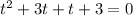
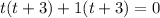
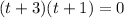
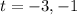
The zeros of the function is at t=-3,-1.

2) The vertex of the parabola,

Comparing
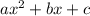`ax^2+bx+c` with
`t^2+4t+3`

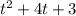
Here, a=1, b=4, c=3

The x -coordinate of the vertex is given by
`-(b)/(2a)`

`-(b)/(2a)=-(4)/(2(1))=-2`

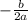
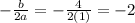
For y-coordinate put t=-2 in the function,

`h(-2)=(-2)^2+4(-2)+3`

`h(-2)=4-8+3`

`h(-2)=-1`

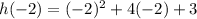
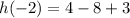
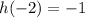
The vertex of the parabola is (-2,-1).