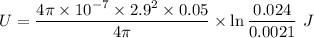Question

What is the magnetic potential energy stored in a cylindrical volume of height hcylin = 50 mm and radius Rcylin = 24 mm that symmetrically surrounds an infinitely long wire that has radius Rwire = 2.1 mm and carries current I = 2.9 A ? The volume in which the energy should be calculated does not contain the wire

Answer 1

`U=1.02* 10^(-7)\ J`

Step-by-step explanation:

Given that

h= 50 mm = 0.05 m

R= 24 mm = 0.024 m

Rw= 2.1 mm = 0.0021 m

I= 2.9 A

We know that magnetic filed given as

`B=(\mu _oI)/(2\pi r)`

Volume of small element

dV= 2πr hdr

Now the magnetic potential energy given as

`U=\int (B^2)/(2\mu_o)dV`

`B=(\mu _oI)/(2\pi r)`

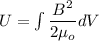
dV= 2πr hdr

`U=\int(\left((\mu _oI)/(2\pi r)\right)^2)/(2\mu_o)2\pi rhdr`

`U=(\mu _oI^2h)/(4\pi)\int_(R_w)^(R)(dr)/(r)`

`U=(\mu _oI^2h)/(4\pi)* \ln(R)/(R_w)`

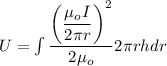
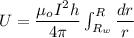
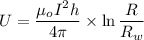
Now by putting the values

`U=(4\pi * 10^(-7)* 2.9^2* 0.05)/(4\pi)* \ln(0.024)/(0.0021)\ J`

`U=1.02* 10^(-7)\ J`