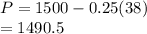Question

Suppose that each day a company has fixed costs of 400 dollars and variable costs of 0.8x+1420 dollars per unit, where x is the number of units produced that day. Suppose further that the selling price of its product is 1500−0.25x dollars per unit.

a) each day, the company breaks even at production levels (blank) units
b) the maximum daily revenue attained is (blank) dollars
c) the price that maximizes profit is (blank) dollars per unit

Answer 1

Explanation:

Given that a company fixed costs are 400 dollars

and variable cost =
`0.8x+1420` per unit and x the no of units produced

Selling price =
`1500-0.25x` per unit

a) Break even units

At break even units selling price = variable cost

`1500-0.25x=0.8x+1420\\1.05x = 80\\x=76.19~76`

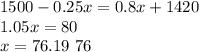
Break even units = 76

b) Revenue = Sales - total costs

=
`x(1500-0.25x)-(x)(0.8x+1420)-400\\= 1500x-0.25x^2-0.8x^2-1420x-400\\= -1.05x^2+80x-400`

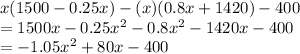
Use derivative test to get max revenue

R'(x) =
`-2.10x+80`

R"(X) <0

So maximum when I derivative =0 or when

`x=38.10`

x=38

c) price when x =38 is

`P = 1500-0.25(38)\\=1490.5`