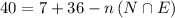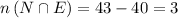Question

In a class of 40 students, everyone has either a pierced nose or a pierced ear. The professor asks everyone with a pierced nose to raise his or her hand. Seven hands go up. Then the professor asked everyone with a pierced ear to do likewise. This time there are 36 hands raised. How many students have piercings both on their ears and their noses?I would think the obvious answer could be 7 but not necessarily. Can anyone help me with this formula?

Answer 1

Answer:3

Explanation:

Given

There are total 40 students in a class

No of students with Pierced Nose n(N)=7

No of students with Pierced ear n(E)=36

and we know using sets

`n\left ( N\cup E\right )=n\left ( E\right )+n\left ( N\right )-n\left ( N\cap E\right )`

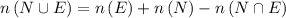
where
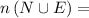`n\left ( N\cup E\right )=`Students either nose or ear Pierced

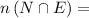`n\left ( N\cap E\right )=`no of students having both nose and ear pierced

`40=7+36-n\left ( N\cap E\right )`

`n\left ( N\cap E\right )=43-40=3`