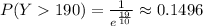Question

The operator of a pumping station has observed that demand for water during early afternoon hours has an approximately exponential distribution with mean 100 cfs (cubic feet per second). (a) Find the probability that the demand will exceed 190 cfs during the early afternoon on a randomly selected day. (Round your answer to four decimal places.)

Answer 1

The probability that the demand will exceed 190 cfs during the early afternoon on a randomly selected day is
`P(Y>190)=\frac{1}{e^{(19)/(10)}}\approx 0.1496`

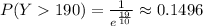
Explanation:

Let Y be the water demand in the early afternoon.

If the random variable Y has density function f (y) and a < b, then the probability that Y falls in the interval [a, b] is

`P(a\leq Y \leq b)=\int\limits^a_b {f(y)} \, dy`

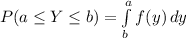
A random variable Y is said to have an exponential distribution with parameter
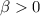`\beta > 0` if and only if the density function of Y is

`f(y)=\left \{ {{(1)/(\beta)e^{-(y)/(\beta) }, \quad{0\:\leq \:y \:\leq \:\infty}   } \atop {0}, \quad elsewhere} \right.`

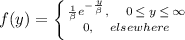
If Y is an exponential random variable with parameter β, then

mean = β

To find the probability that the demand will exceed 190 cfs during the early afternoon on a randomly selected day, you must:

We are given the mean = β = 100 cubic feet per second

`P(Y>190)=\int\limits^(\infty)_(190) {(1)/(100)e^(-y/100) } \, dy`

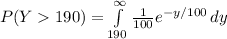
Compute the indefinite integral
`\int (1)/(100)e^{-(y)/(100)}dy`

`(1)/(100)\cdot \int \:e^{-(y)/(100)}dy\\\\\mathrm{Apply\:u \:substitution}\:u=-(y)/(100)\\\\(1)/(100)\cdot \int \:-100e^udu\\\\(1)/(100)\left(-100\cdot \int \:e^udu\right)\\\\(1)/(100)\left(-100e^u\right)\\\\\mathrm{Substitute\:back}\:u=-(y)/(100)\\\\(1)/(100)\left(-100e^{-(y)/(100)}\right)\\\\-e^{-(y)/(100)}`

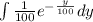
Compute the boundaries

`\int _(190)^(\infty \:)(1)/(100)e^{-(y)/(100)}dy=0-\left(-\frac{1}{e^{(19)/(10)}}\right)`

`\int _(190)^(\infty \:)(1)/(100)e^{-(y)/(100)}dy=\frac{1}{e^{(19)/(10)}}\approx 0.1496`

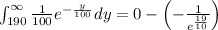
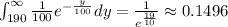
The probability that the demand will exceed 190 cfs during the early afternoon on a randomly selected day is
`P(Y>190)=\frac{1}{e^{(19)/(10)}}\approx 0.1496`