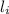Answer:
Initial area of the specimen

Where,
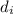 is the initial diameter of the metal specimen.
is the initial diameter of the metal specimen.
Substituting
 for
for
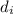

Final minimum area of the specimen
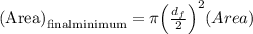
Where
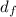 is final minimum diameter.
is final minimum diameter.
Substituting
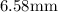 for
for
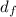
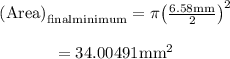
Percentage reduction in the area.

Substituting
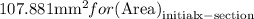 and
and
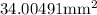 for
for
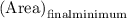

(b)
The expression for the percent increase in the gauge length of the specimen.
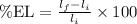
Substituting
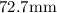 for
for
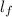 and
and
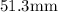 for
for