Question

A factory has three types of machines, each of which works at its own constant rate. If 7 Machine As and 11 Machine Bs can produce 250 widgets per hour, and if 8 Machine As and 22 Machine Cs can produce 600 widgets per hour, how many widgets could one machine A, one Machine B, and one Machine C produce in one 8-hour day?

A. 400
B. 475
C. 550
D. 625
E. 700

Answer 1

A. 400

Explanation:

Although it seems a difficult at first, this problem can be solved in fairly simple manner. First, write down the equations given by the problem:

`7A + 11B = 250\\8A +22C=600`

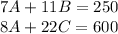
There we have 3 unknown values and only 2 equations so it can't be solved as a common system problem. However, if we double the first equation and add it to the second one, it yields:

`8A + 22C +14 A + 22B=600 + 500\\22A+22B+22C = 1100\\A+B+C = 50`

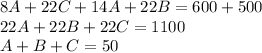
Therefore, one machine A, one Machine B, and one Machine C produce 50 widgets per hour, so in one 8-hour day they produce:

`P= 8 * 50 = 400`