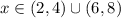Answer:
9. c.
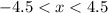
9. e.

9. f.
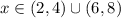
Explanation:
9. c. Given
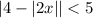
Rewrite it as follows:
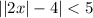
This inequality is equivalent ot the double inequality
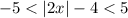
Add 4:
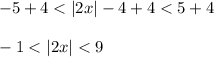
But the absolute value |2x| is always no less than 0, so
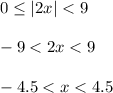
9. e. Given
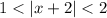
This inequality is equivalent to
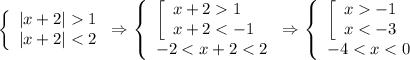
So,

9. f. Given
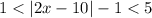
Add 1:

This inequality is equivalent to
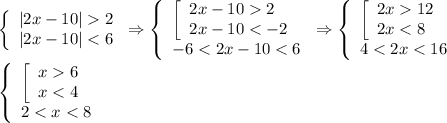
So,