Question

A fair die is rolled twice. What is the probability that: a. The die shows a different number on each toss. e.g. (2,5) b. The sum of the dots showing is greater than or equal to 10. List the outcomes in this set. Then calculate the probability. c. The total score is less than 4. List the outcomes in this set. Then calculate the probability.

Answer 1

a)
`(5)/(6)`

b)
`(1)/(6)`

c)
`(1)/(9)`

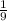
Explanation:

Total possible outcomes when a dice is rolled twice

(1,1) , (1,2) , (1,3) , (1,4) , (1,5) , (1,6)

(2,1) , (2,2) , (2,3) , (2,4) , (2,5) , (2,6)

(3,1) , (3,2) , (3,3) , (3,4) , (3,5) , (3,6)

(4,1) , (4,2) , (4,3) , (4,4) , (4,5) , (4,6)

(5,1) , (5,2) , (5,3) , (5,4) , (5,5) , (5,6)

(6,1) , (6,2) , (6,3) , (6,4) , (6,5) , (6,6)

here total number of possible outcomes is 36

now,

P (Event ) =
`\frac{\textup{Number of favorable outcomes of an Event}}{\textup{Total possible outcomes}}`

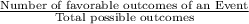
a) P( die shows a different number on each toss )

Favorable outcomes = (1,2) , (1,3) , (1,4) , (1,5) , (1,6) , (2,1) , (2,3) , (2,4) , (2,5) , (2,6), (3,1) , (3,2) , (3,4) , (3,5) , (3,6) , (4,1) , (4,2) , (4,3) , (4,5) , (4,6) , (5,1) , (5,2) , (5,3) , (5,4) , (5,6) , (6,1) , (6,2) , (6,3) , (6,4) , (6,5)

number of Favorable outcomes = 30

thus,

P( die shows a different number on each toss ) =
`(30)/(36)=(5)/(6)`

b) P( The sum of the dots showing is greater than or equal to 10 )

Favorable outcomes = (4,6) , (5,5) , (5,6) , (6,4) , (6,5) , (6,6)

number of Favorable outcomes = 6

P( The sum of the dots showing is greater than or equal to 10 )

=
`(6)/(36)=(1)/(6)`

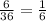
c) P( total score is less than 4 )

Favorable outcomes = (1,1) , (1,2) , (1,3) , (2,1)

number of Favorable outcomes = 4

P( total score is less than 4 ) =
`(4)/(36)=(1)/(9)`