Answer:
(a)
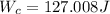
(b)
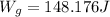
(c) K.E. = 21.168 J
(d)
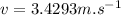
Step-by-step explanation:
Given:
- mass of a block, M = 3.6 kg
- initial velocity of the block,
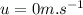
- constant downward acceleration,
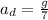
 That a constant upward acceleration of
That a constant upward acceleration of
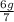 is applied in the presence of gravity.
is applied in the presence of gravity.
∴

- height through which the block falls, d = 4.2 m
(a)
Force by the cord on the block,
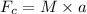
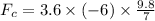

∴Work by the cord on the block,

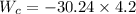
We take -ve sign because the direction of force and the displacement are opposite to each other.
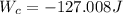
(b)
Force on the block due to gravity:
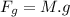
∵the gravity is naturally a constant and we cannot change it
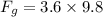

∴Work by the gravity on the block,
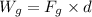
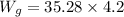
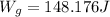
(c)
Kinetic energy of the block will be equal to the net work done i.e. sum of the two works.
mathematically:
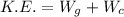
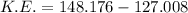
K.E. = 21.168 J
(d)
From the equation of motion:

putting the respective values:
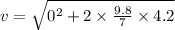
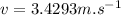 is the speed when the block has fallen 4.2 meters.
is the speed when the block has fallen 4.2 meters.