Question

A submarine travels 6.6 km due West from its base and then turns and travels due South for 3.9

km.
How far away is the submarine from its base?
Give your answer rounded to 1 DP.

Answer 1

`7.7` km

Explanation:

The submarine's path from its base forms a right triangle when its final position is "connected" to the base. We know that the right triangle has legs of
`6.6` km and
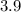`3.9` km, and we need to find the length of its hypotenuse. To do so, we can use the Pythagorean Theorem, which states that in a right triangle,
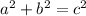`a^(2)+b^(2) =c^(2)`, where
`a` and
`b` are the lengths of the triangle's legs and
`c` is the length of the triangle's hypotenuse. In this case, we know what
`a` and
`b` are, and we need to solve for c, so after substituting the given values of
`a` and
`b` into
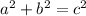`a^(2)+b^(2) =c^(2)` to solve for c, we get:

`a^(2)+b^(2) =c^(2)`

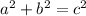
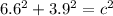`6.6^(2) +3.9^(2) =c^(2)` (Substitute
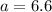`a=6.6` and
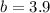`b=3.9` into the equation)

`43.56+15.21=c^(2)` (Evaluate the squares on the LHS)

`58.77=c^(2)` (Simplify the LHS)

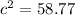`c^(2)=58.77` (Symmetric Property of Equality)

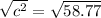`\sqrt{c^(2) } =√(58.77)` (Take the square root of both sides of the equation)

`c=7.7,c=-7.7` (Simplify)

`c=-7.7` is an extraneous solution because you can't have negative distance, if that makes sense, so therefore, the submarine is approximately
`7.7` km away from its base. Hope this helps!