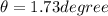Question

A ladder is leaning against a vertical wall, and both ends of the ladder are at the point of slipping. The coefficient of friction between the ladder and the horizontal surface is μ₁ = 0.115 and the coefficient of friction between the ladder and the wall is μ₂ = 0.103. Determine the maximum angle with the vertical the ladder can make without falling on the ground.

Answer 1

`\theta = 1.73 degree`

Step-by-step explanation:

Let the ladder makes some angle with the horizontal

now by force balance in x direction we have

`F_(f1) = N_2`

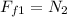
in Y direction force balance is given as

`F_(f2) + N_1 = mg`

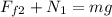
now we know that

`F_(f1) = 0.115 N_1`

`F_(f2) = 0.103 N_2`

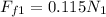
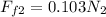
also by torque balance we have

`N_2(Lcos\theta) + 0.103N_2(Lsin\theta) = mg((L)/(2) cos\theta)`

`0.115 N_1 = N_2`

`0.103 N_2 + N_1 = mg`

`(0.103)(0.115 N_1) + N_1 = mg`

`1.012 N_1 = mg`

`N_1 = 0.988 mg`

`N_2 = 0.113 mg`

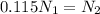
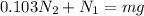
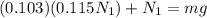
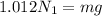
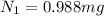
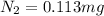
now from above equation

`(0.113 mg)cos\theta + (0.103)(0.113mg) sin\theta = (mg)/(2) cos\theta`

`0.113 + 0.0117 tan\theta = 0.5`

`\theta = 88.3 degree`

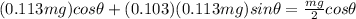
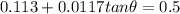
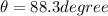
so angle with the vertical is given as

`\theta = 1.73 degree`