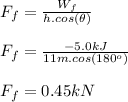Answer:
a)
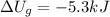
b)
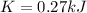
c)
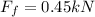
Step-by-step explanation:
the gravitational potential energy is given by:
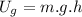
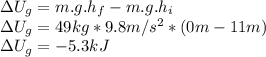
The kinetic energy is given by:
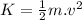
the initial kinetic energy is zero because the motion started from rest, so:

applying the conservation of energy theorem:
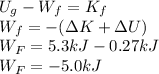
The work done by the friction force is given by:
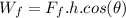
the angle of the force is 180 degrees because it's against the movement: