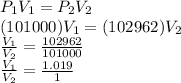Question

A bubble, located 0.200 m beneath the surface in a glass of beer, rises to the top. The air pressure at the top is 1.01x10⁵ Pa. Assume that the density of beer is the same as that of fresh water. If the temperature and number of moles of CO₂ in the bubble remain constant as the bubble rises, find the ratio of the bubble's volume at the top to its volume at the bottom.

Answer 1

`(1.019)/(1)`

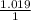
Step-by-step explanation:

To solve this equation we will have to consider that the bubble is filled with an Ideal Gas and as such we can use the Ideal Gas Law

`PV = nRT`

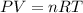
Where

`P` = Pressure

`V` = Volume

`n` = Moles

`R` = Ideal Gas Constant

`T` = Temperature

Now since we know that the value for the temperature and moles is constant we can simply use Boyles Law for the two states

`P_(1) V_(1) =P_(2) V_(2)`

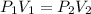
Let us look at the two states

State 1 (at top)

Pressure =
`1.01*10^5`

Volume =
`V_(1)`

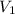
State 2 (at bottom)

Pressure =
`1.01*10^5 + dgh`

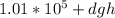
Where

`d` = Density of liquid (1000 kg/m³)

`d` = Acceleration due to gravity (9.8 m/s²)

`d` = Height of liquid (0.200 m)

Pressure =
`102,962`

Volume =
`V_(2)`

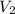
Inputting these values into the Boyles Law

`P_(1) V_(1) =P_(2) V_(2)\\ (101000)V_(1) = (102962)V_(2)\\ (V_(1))/(V_(2)) = (102962)/(101000) \\  (V_(1))/(V_(2)) = (1.019)/(1)`