Question

A boat moves through the water with two forces acting on it. One is a 2.05 ✕ 103 N forward push by a motor, and the other is a 1.87 ✕ 103 N resistive force due to the water.

(a) What is the acceleration of the 1300 kg boat? m/s2 forward
(b) If it starts from rest, how far will it move in 8 s? m (c) What will its speed be at the end of its time interval? m/s

Answer 1

(a) a= 0.139 m/s²

(b) d= 4.45 m

(c) vf= 1.1 m/s

Step-by-step explanation:

a) We apply Newton's second law:

∑F = m*a Formula (1)

∑F : algebraic sum of the forces in Newton (N)

m : mass (kg)

a : acceleration (m/s²)

Data

F₁= +2.05 * 10³ N : forward push by a motor

F₂= -1.87* 10³ N : resistive force due to the water.

m= 1300 kg

Calculation of the acceleration of the boat

We replace data in the formula (1):

∑F = m*a

F₁+F₂= m*a

`a=(F_(1) +F_(2) )/(m)`

`a= (2.05*10^(3) -1.87*10^(3))/(1300)`

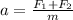
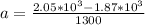
a= 0.139 m/s²

b) Kinematics of the boat

Because the boat moves with uniformly accelerated movement we apply the following formulas:

d= v₀t+ (1/2)*a*t² Formula (2)

vf= v₀+at Formula (3)

Where:

d:displacement in meters (m)

t : time interval (s)

v₀: initial speed (m/s)

vf: final speed (m/s)

a: acceleration (m/s² )

Data

v₀ = 0

a= 0.139 m/s²

t = 8 s

Calculation of the distance traveled by the boat in 8 s

We replace data in the formula (2)

d= v₀t+ (1/2)*a*t²

d= 0+ (1/2)*(0.139)*(8)²

d= 4.45 m

c) Calculation of the speed of the boat in 8 s

We replace data in the formula (3):

vf= v₀+at

vf= 0+( 0.139)*(8)

vf= 1.1 m/s