Question

A single conservative force acts on a 5.30-kg particle within a system due to its interaction with the rest of the system. The equation

Fx = 2x + 4
describes the force, where Fx is in newtons and x is in meters. As the particle moves along the x axis from x = 1.08 m to x = 6.50 m, calculate the following.
(a) the work done by this force on the particle
1 J
(b) the change in the potential energy of the system
2 J
(c) the kinetic energy the particle has at x = 6.50 m if its speed is 3.00 m/s at x = 1.08 m
3 J

Answer 1

Given that

m = 5.3 kg

Fx = 2x + 4

We know that work done by force F given as

w= ∫ F. dx

a)

Given that x=1.08 m to x=6.5 m

Fx = 2x + 4

w= ∫ F. dx

`w=\int_(1.08)^(6.5)(2x+4) .dx`

`w=\left [x^2+4x \right ]_(1.08)^(6.5)`

`w=(6.5^2-1.08^2)+4(6.5-1.08)\ J`

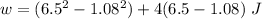
w=62.7 J

b)

We know that potential energy given as

`F=-(dU)/(dx)`

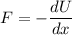
∫ dU = -∫F.dx ( w= ∫ F. dx)

ΔU= -62.7 J

c)

We know that form work power energy theorem

Net work = Change in kinetic energy

W= KE₂ - KE₁

62.7 =KE₂ - (1/2)x 5.3 x 3²

KE₂ = 86.55 J

This is the kinetic energy at 6.5m